I quadrilateri – mappa concettuale
Clikka sui vari quadrilateri per avere più informazioni e avere il link alla videolezione!
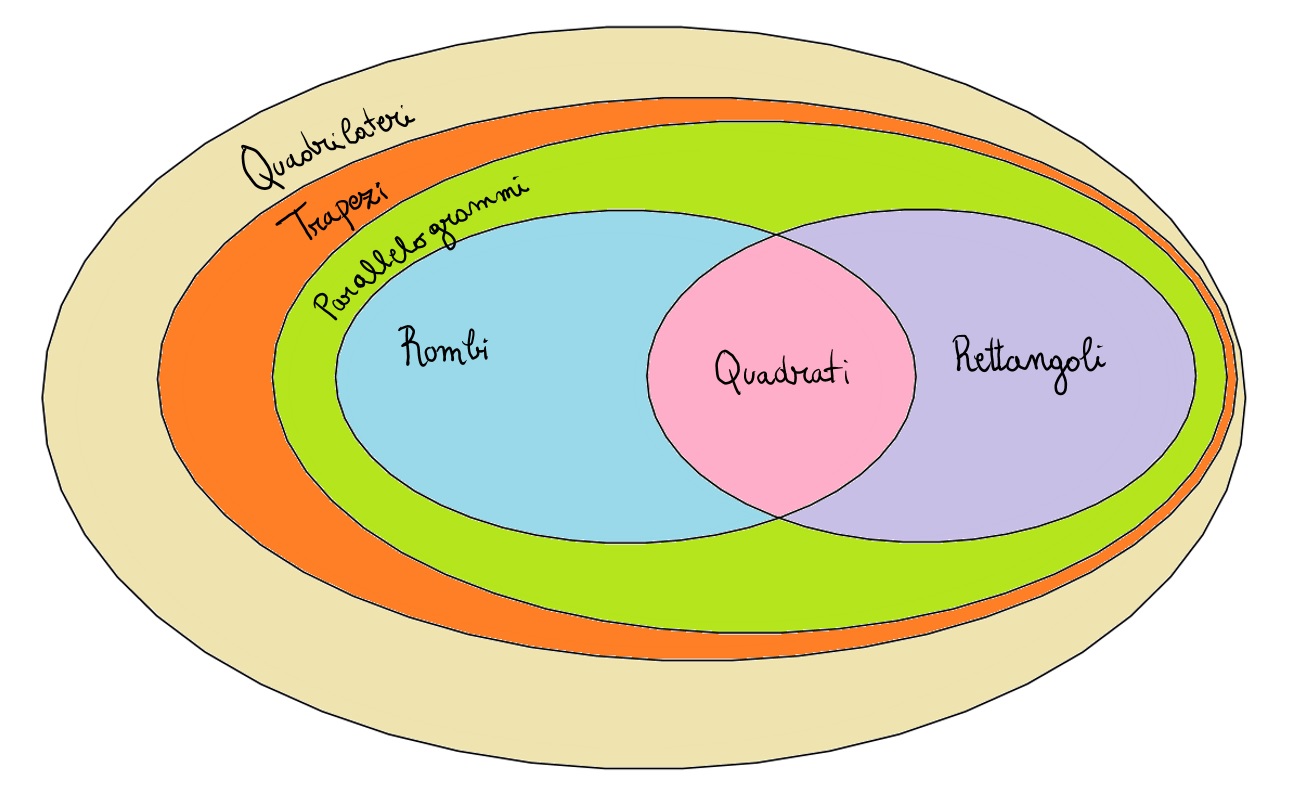
I quadrilateri
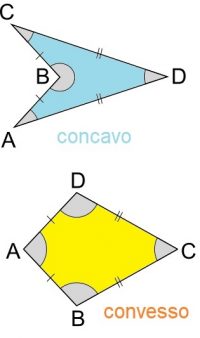
Caratteristiche:
- 4 lati
- 4 angoli interni
- 2 diagonali
- somma degli angoli interni = 360°
- possono essere concavi o convessi
Quadrilatero concavo: il poligono contiene il prolungamento dei lati
Quadrilatero convesso: il poligono non contiene il prolungamento dei lati
Definizione di quadilatero:
Poligono di quattro lati
Definizione di poligono:
Parte di piano delimitata da una linea spezzata chiusa
I trapezi
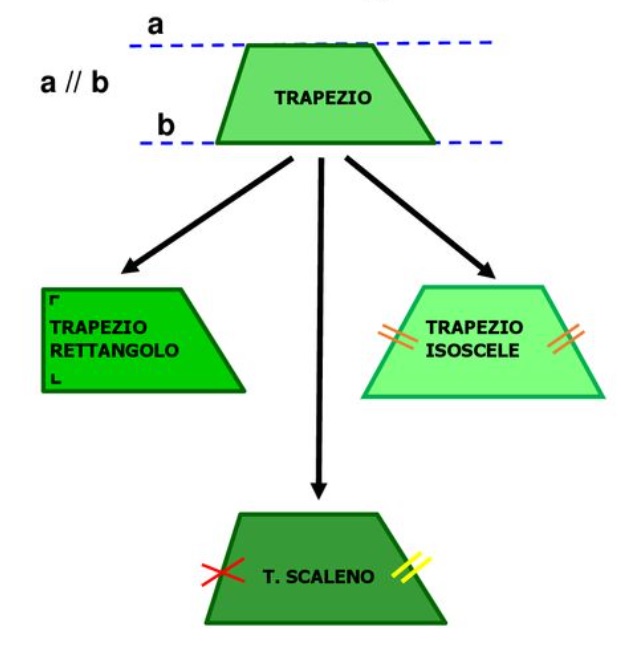
Caratteristiche:
- I trapezi, essendo dei quadrilateri (sono un sottoinsieme), godono di tutte le proprietà/caratteristiche dei quadrilateri ossia hanno:
- 4 lati
- 4 angoli interni la cui somma da 360°
- 2 diagonali
- E in più hanno:
- Due lati opposti paralleli
- angoli adiacenti al lato obliquo supplementari (somma 180°)
Definizione di Trapezio
- Quadrilatero con due lati opposti paralleli
Definizione di Quadrilatero:
- Poligono di quattro lati
Parallelogrammi
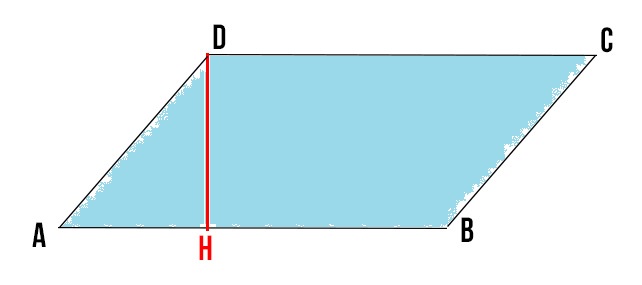
Caratteristiche:
I parallelogrammi, essendo dei trapezi (sono un sottoinsieme dei trapezi a loro volta sono un sottoinsieme dei quadrilateri), godono di tutte le proprietà/caratteristiche dei trapezi e quindi anche dei quadrilateri ossia hanno:
- 4 lati, 4 angoli interni la cui somma da 360°, 2 diagonali
- Una coppia di lati opposti paralleli
- Angoli adiacenti al lato obliquo supplementari (somma 180°)
e in più hanno:
- anche l'altra coppia di lati paralleli tra loro (quindi in totale hanno due coppie di lati opposti paralleli)
- i lati opposti oltre ad essere paralleli sono anche sono congruenti
- gli angoli opposti sono congruenti
- gli angoli adiacenti a qualsiasi lato sono supplementari
- le diagonali si tagliano scambievolmente a metà
Definizione di parallelogramma:
Verrebbe da dire che il parallelogramma è un trapezio con due coppie di lati opposti paralleli.
Ma avendo il trapezio già una coppia di lati opposti paralleli la definizione sopra contiene una "ripetizione". Per non ripetersi occorrerebbe specificare che il parallelogramma è un trapezio avente anche l'altra coppia di lati opposti paralleli tra loro ma a livello linguistico sentite bene che si parla di "l'altra coppia" senza aver menzionato la prima. La soluzione più semplice è quindi partire sempre dal quadrilatero:
"Il parallelogramma è il quadrilatero avente due coppie di lati opposti paralleli"
I rombi
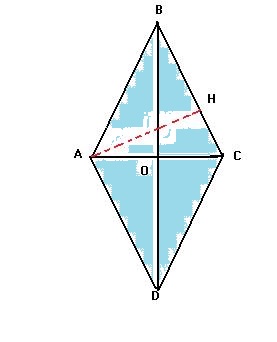
Caratteristiche:
I rombi, essendo dei parallelogrammi (sono un sottoinsieme dei parallelogrammi che a loro volta sono un sottoinsieme dei trapezi che a loro volta sono un sottoinsieme dei quadrilateri), godono di tutte le proprietà/caratteristiche dei parallelogrammi, e quindi anche dei trapezi e dei quadrilateri e quindi per cominciare riassumiamo:
- 4 lati, 4 angoli interni la cui somma da 360°, 2 diagonali
- Due coppie di lati opposti paralleli e congruenti (NB: se sono congruenti sono anche paralleli e viceversa)
- Angoli adiacenti a qualsiasi lato supplementari (somma 180°)
- gli angoli opposti sono congruenti
- le diagonali si tagliano scambievolmente a metà
In più hanno:
- le diagonali sono tra loro perpendicolari
- tutti i lati sono tra loro congruenti
Definizione di rombo:
Verrebbe da dire che il rombo è un parallelogramma con tutti i lati congruenti tra loro, ma avendo il parallelogramma i lati congruenti a due a due vi è una ripetizione. Anche qui per evitare ripetizioni si parte dai quadrilateri dicendo:
"Il rombo è il quadrilatero avente tutti i lati congruenti tra loro"
Questa proprietà è bastante ad identificare il rombo in quanto da essa ne derivano tutte le altre. E' infatti possibile dimostrare che se tutti i lati sono congruenti tra loro sono anche paralleli a due a due e che le diagonali sono tra loro perpendicolari e si tagliano scambievolmente a metà e che anche gli angoli opposti sono congruenti.
Altra definizione:
"Il rombo è il parallelogramma con le diagonali perpendicolari tra loro."
Si può definire il rombo infatti anche a partire dalle diagonali. Infatti se prendiamo un quadrilatero con le diagonali perpendicolari e che si tagliano scambievolmente a metà non può che essere un rombo e perciò questa caratteristica è sufficiente a identificare la figura e quindi a derivarne tutte le altre proprietà, ossia la congruenza dei lati, gli angoli opposti congruenti, il parallelismo dei lati opposti...
I rettangoli

Caratteristiche:
I rettangoli, essendo dei parallelogrammi (sono un sottoinsieme dei parallelogrammi che a loro volta sono un sottoinsieme dei trapezi a loro volta sono un sottoinsieme dei quadrilateri), godono di tutte le proprietà/caratteristiche dei parallelogrammi, dei trapezi e dei quadrilateri ossia hanno:
- 4 lati, 4 angoli interni la cui somma da 360°, 2 diagonali
- Due coppie di lati opposti paralleli e congruenti (NB: se sono congruenti sono anche paralleli e viceversa)
- Angoli adiacenti a qualsiasi lato supplementari (somma 180°)
- gli angoli opposti sono congruenti
- le diagonali si tagliano scambievolmente a metà
In più hanno
- Tutti gli angoli interni congruenti tra loro e quindi da 90° cioè retti (in quanto la somma deve essere 360°)
- Le diagonali sono congruenti tra loro
Definizioni di rettangolo:
Verrebbe da dire che il rettangolo è il parallelogramma con tutti gli angoli interni retti. Ma questa caratteristica è bastante anche se al posto di parallelogramma scriviamo quadrilatero. Infatti
"un qualsiasi quadrilatero con gli angoli interni retti è un rettangolo"
così come
"un qualsiasi quadrilatero con le diagonali congruenti e che si tagliano scambievolmente a metà è sempre un rettangolo".
Queste due condizioni sono per sé stesse sufficienti per identificare un rettangolo. Basti pensare al contrario, ossia se è possibile costruire un'altra figura che non sia un rettangolo ma che abbia invece 4 angoli interni retti o le diagonali congruenti e che si tagliano scambievolmente a metà. Se non è possibile farlo (perché possiamo costruire solo rettangoli) vuol dire che queste sono condizioni sufficienti.
I quadrati
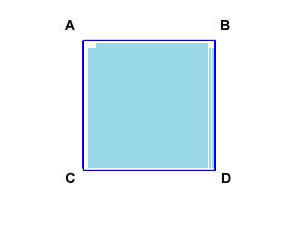
Vai alla videolezione
Caratteristiche:
I quadrati, essendo dei rettangoli e contemporaneamente rombi. E' l'insieme intersezione dei due insiemi dei rombi e dei rettangoli, quindi essendo gli elementi in comune dei due insiemi godono delle proprietà di entrambi! Ossia tutti i quadrati sono rombi, e tutti i quadrati sono anche rettangoli! Inoltre sono un sottoinsieme ovviamente anche dei parallelogrammi che a loro volta sono un sottoinsieme dei trapezi a loro volta sono un sottoinsieme dei quadrilateri, e quindi godono di tutte le proprietà/caratteristiche dei rombi, rettangoli, parallelogrammi, trapezi e quadrilateri ossia hanno:
- 4 lati, 4 angoli interni la cui somma da 360°, 2 diagonali
- I lati opposti sono paralleli
- Angoli adiacenti a qualsiasi lato supplementari (somma 180°)
- Tutti gli angoli interni sono congruenti tra loro (non solo gli opposti)
- le diagonali sono tra loro perpendicolari, congruenti e si tagliano scambievolmente a metà
- Tutti i lati sono tra loro congruenti
Per definire un quadrato possiamo partire dal rombo e aggiungendo una caratteristica propria ai rettangoli per esempio dicendo:
E' un rombo avente tutti gli angoli interni congruenti tra loro
oppure
E' un rombo avente le diagonali congruenti tra loro
Oppure possiamo partire dal rettangolo e aggiungere una caratteristica del rombo, ad esempio:
E' un rettangolo avente le diagonali tra loro perpendicolari
oppure
E' un rettangolo avete tutti i lati tra loro congruenti
Oppure possiamo partire dal parallelogramma ed aggiungere una caratteristica propria ai rombi e ai rettangoli ad esempio:
è un parallelogramma con tutti gli angoli congruenti tra loro e con le diagonali tra loro perpendicolari
e via dicendo.