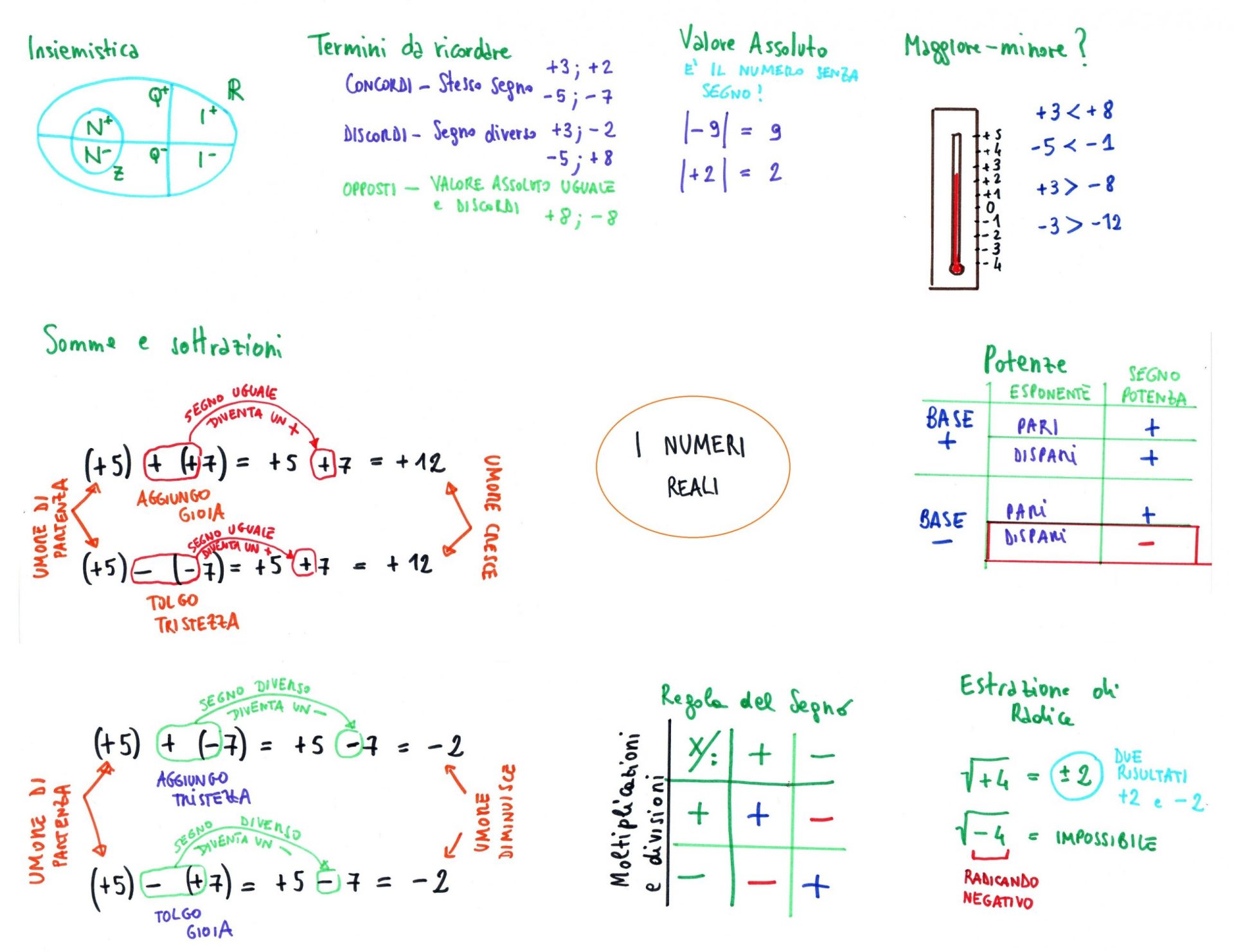
I numeri Reali - mappa concettuale interattiva

Insiemistica

N+ = N insieme dei numeri Naturali (interi e positivi)

N- = insieme dei numeri interi e negativi

Z = N+ + N- = è l'insieme dei numeri interi siano essi positivi che negativi

Q è l'insieme dei numeri Razionali ossia numeri rappresentabili da Frazioni. In questo insieme si possono trovare numeri positivi e negativi, decimali limitati e periodici, numeri interi, frazioni... Notare che N è sottoinsieme di Z che a sua volta è sottoinsieme di Q.

I è l'insieme dei numeri irrazionali, ossia decimali illimitati NON periodici. Le radici di quadrati non perfetti sono numeri irrazionali. Sempre in questo insieme troviamo Pi Greco , il numero di Eulero e molti altri.

R è l'insieme dei numeri Reali, ossia la somma degli insiemi Q e I.

infatti Q + I = R

ma è vero anche che Q è sottoinsieme di R come I è sottoinsieme di R in quanto interamente contenuti.

Fuori dall'insieme R troviamo i numeri immaginari, ossia quelli che permettono di risolvere calcoli impossibili. La radice di un radicando negativo per esempio è risolvibile con i numeri immaginari.